Maximum Weighted Independent Set/Clique

The maximum independent set problem and its complement, the maximum clique are among fundamental problems in combinatorial optimization with ubiquitous applications and connections to other problems (Bomze et al.1, Wu and Hao2).

In this Mod, we consider the more general problems of the maximum weighted independent set and maximum weighted clique which have applications in various fields such as computer vision, pattern recognition, molecular structure matching, social network analysis, and genome data mapping. To better understand how a theoretical graph theory problem can be used to address a real-world challenge, let us review one application area for each problem in detail.

Maximum weighted independent set: To measure the structural similarity between two molecules, the molecules are first represented as labeled graphs where the vertices and the edges correspond to the atoms of the molecule and its chemical bonds, respectively. To find the largest substructure (subgraph) that appears in both molecular graphs, it suffices to find the maximum weighted independent set of a third graph, known as conflict graph. The vertices and the edges of the conflict graph represent possible mappings and conflicts between two molecules, respectively.

Maximum weighted clique: Consider a social network where the people and the connections between them are respectively represented as vertices and the edges of a graph. Different social and psychological behavior of people are also taken into account as vertex weights. To find a group of people who all know each other and have the maximum social/psychological harmony, it suffices to identify the maximum weighted clique of the social graph.

Problem Specification

Maximum weighted independent set: Consider an undirected graph \(G\) with \(n\) vertices and \(m\) edges where each vertex is associated with a positive weight \(w\). Find a maximum weighted independent set, i.e., select a set of vertices in graph \(G\) where there is no edge between any pair of selected vertices and the sum of the vertex weights for this set is maximised.

More formally stated, let \(G = (V, E, w)\) be an undirected graph where each vertex \(i \in V\) has a positive weight \(w_i\). Find a subset \(S \subseteq V\) such that:

• no two vertices in \(S\) are connected by an edge; and

• among all such independent sets, the set \(S\) has the maximum total vertex weight.

Note: In case all vertices have equal weights, the cardinality of set \(S\) represents the stability number of graph \(G\).

Background: Optimization Model

This Mod is implemented by formulating a Binary Integer Programming (BIP) model and solving it using Gurobi. For each vertex \(i \in V\), define a binary decision variable \(x_i\) as below:

\[\begin{split}x_i = \begin{cases} 1 & \text{if vertex}\,i\,\text{belongs to set}\,S\,\\ 0 & \text{otherwise.} \\ \end{cases}\end{split}\]

The formulation of the MWIS is then given below:

\[\begin{split}\begin{align} \max \quad & \sum_{i \in V} w_i x_i \\ \mbox{s.t.} \quad & x_i + x_j \leq 1 & \forall (i, j) \in E \\ & x_i \in \{0, 1\} & \forall i \in V \end{align}\end{split}\]

Maximum weighted clique: Given an undirected graph \(G = (V, E, w)\), finding the maximum weighted clique of graph \(G\) is equivalent to finding the maximum weighted independent set of its complement graph \(G^{\prime} = (V, E^{\prime}, w)\) where

• for every edge \((i, j)\) in \(E\), there is no edge in \(E^{\prime}\), and

• for every edge \((i, j)\) not in \(E\), there is an edge in \(E^{\prime}\).

Note: In case all vertices have equal weights, the cardinality of the maximum clique set represents the clique number of graph \(G\).

Interface

The functions maximum_weighted_independent_set and maximum_weighted_clique support scipy sparse matrix/array, networkx graph, and pandas dataframes as possible input graph. The input graph captures the adjacency matrix of the graph \(G\) (upper triangle with zero diagonals only). The user should also provide the vertex weights as a numpy array or a pandas dataframe depending on the input graph data structure.

The example below finds the maximum weighted independent set and the maximum weighted clique for a graph with 8 vertices and 12 edges known as the cube graph.

scipy.sparsenetworkxpandas

The input graph and the vertex weights are provided as a scipy sparse array and a numpy array, respectively.

import scipy.sparse as sp
import networkx as nx
import numpy as np
from gurobi_optimods.mwis import maximum_weighted_independent_set, maximum_weighted_clique

# Graph adjacency matrix (upper triangular) as a sparse array.
g = nx.cubical_graph()
graph_adjacency = sp.triu(nx.to_scipy_sparse_array(g))
# Vertex weights
weights = np.array([2**i for i in range(8)])

# Compute maximum weighted independent set.
mwis = maximum_weighted_independent_set(graph_adjacency, weights)

# Compute maximum weighted clique.
mwc = maximum_weighted_clique(graph_adjacency, weights)

Solution

Independent of the input types, the solution is always a data class including the numpy array of the vertices in the independent set or clique as well as its weight.

>>> mwis
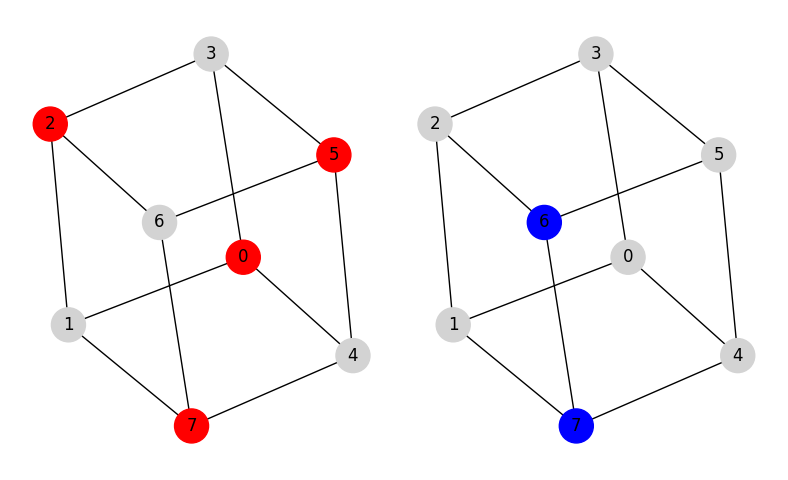
Result(x=array([0, 2, 5, 7]), f=165)
>>> mwis.x
array([0, 2, 5, 7])
>>> mwis.f
165

>>> mwc
Result(x=array([6, 7]), f=192)
>>> mwc.x
array([6, 7])
>>> mwc.f
192

import networkx as nx
import matplotlib.pyplot as plt

fig, (ax1, ax2) = plt.subplots(1, 2)
layout = nx.spring_layout(g, seed=0)

# Plot the maximum weighted independent set
color_map = ["red" if node in mwis.x else "lightgrey" for node in g.nodes()]
nx.draw(g, pos=layout, ax= ax1, node_color=color_map, node_size=600, with_labels=True)

# Plot the maximum weighted clique
color_map = ["blue" if node in mwc.x else "lightgrey" for node in g.nodes()]
nx.draw(g, pos=layout, ax = ax2, node_color=color_map, node_size=600, with_labels=True)

fig.tight_layout()
plt.show()

The vertices in the independent set and in the clique are highlighted in red and blue, respectively.

1

Immanuel M Bomze, Marco Budinich, Panos M Pardalos, and Marcello Pelillo. The maximum clique problem. Handbook of Combinatorial Optimization: Supplement Volume A, pages 1–74, 1999.

2

Qinghua Wu and Jin-Kao Hao. A review on algorithms for maximum clique problems. European Journal of Operational Research, 242(3):693–709, 2015.